LTC(Linearly Transformed Cosines)

---
# abstract

> - Linear Transformed Spherical Distribution(LTSD, 线性变换球面分布)。
> - Linear Transformed Cosines(LTC，线性余弦变换)。
>   - M矩阵(逆矩阵/归一化/bake lut)。**描述bsdf形状**。
>   - roughness / anisotropy / skewness。
>   - Nelder–Mead method(downhill simplex method)，下降单纯形法。
> - Shading -- 多边形边积分(非面积积分)。
>   - Stoke’s theorem。
> - 水平面裁剪。
>   - if-else check。
>   - proxy sphere to lut by vector form factor(vector irradiance)。
> - Fresnel修正(bake lut2)。**描述bsdf大小**。
>   - like split sum dfg lut。

---
# LTSD

对于一个球面分布，可以使用一个3x3的矩阵对它的方向向量(即该分布的自变量参数)进行线性变换，从而将其转为另一个球面分布。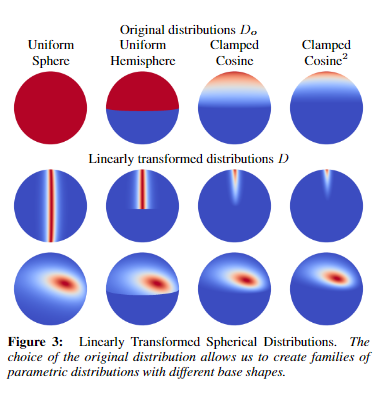

![title](/api/file/getImage?fileId=66358e5ec6875d1c89a1d829)

设
> - $\omega_{0}$。原分布的方向向量(输入)。
> - $M$。线性变换矩阵。
> - $\omega$。变换后的方向向量。

则有

$$
    \omega   = \frac{M \omega_{0}}{|| M \omega_{0} || } \\
    \omega_0 = \frac{M^{-1} \omega}{|| M^{-1} \omega || }
$$

又设
> - $D_0$。原分布。
> - $D$。新分布。

则又有

$$
\begin{aligned}
    D(\omega) &= D_0(\omega_0) \frac{\partial \omega_0}{\partial \omega} \\
              &= D_0(\frac{M^{-1} \omega}{|| M^{-1} \omega ||}) 
                    \frac{M^{-1}}{|| M^{-1} \omega || ^{3}}
\end{aligned}
    \tag{1.1}
$$

其中$\frac{\partial \omega_0}{\partial \omega} = \frac{M^{-1}}{|| M^{-1} \omega || ^{3}}$ 为M变换的雅可比行列式(Jacobian)。

## 性质

> 1. 旋转or缩放不改变形状。M为旋转or缩放变换时，雅可比项为1，分布的形状不改变。
 
> 2. 积分形式不变性。
$$
    \int_{\Omega} D(\omega) \mathrm{d}\omega
    = \int_{\Omega} D_0(\omega_0) \frac{\partial \omega_0}{\partial \omega} \mathrm{d}\omega
    = \int_{\Omega} D(\omega_0) \mathrm{d}\omega_0
$$

> 3. 多边形积分结果不变。
在分布$D$上对一个多边形P积分，和在分布$D_0$上对多边形$P_0$积分的结果是一样的，如果$P_0$上的每一个顶点都是由M矩阵的逆矩阵变换而来的话，即$P_0 = M^{-1}P$。

> 4. 重要性采样。
如果$D_0$可以使用IS，则$D$也可以。
而且因为我们知道了Jacobian，所以$D$的pdf也可以求出。

---
# LTC

## 分布

如果$D_0$的分布为`clamped cosine`(切线)，即
$$
    D_0(\omega_0 = (x, y, z)) = \frac{1}{\pi} max(0, \vec{n} \cdot \vec{\omega_0})
$$

又切线空间，$n = (0, 0, 1)$，所以有
$$
    D_0(\omega_0 = (x, y, z)) = \frac{1}{\pi} max(0, z)
$$

而$D$则为基于各种bxdf所组成的分布，用$\rho$表示，有
$$
    D \approx \rho(\omega_v, \omega_l) \cos\theta_l
$$

如果我们能找到一个变换矩阵$M$，它可以将分布$D_0$变换到分布$D$上，那么**在bxdf分布上对多边形积分**就可以转换为**在$D_0$分布上对多边形积分**的问题。

---
## 变换矩阵的形式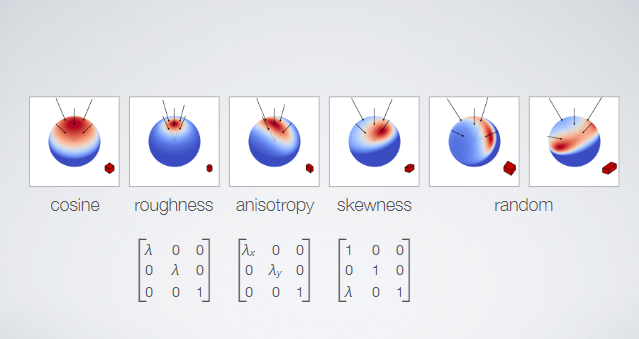

![title](/api/file/getImage?fileId=66359ddec6875d1c89a1d82a)

$$
M =
\begin{bmatrix}
m00 & 0   & m02 \\
  0 & m11 & 0   \\
m20 & 0   & m22
\end{bmatrix}
$$

由于其缩放不改变形状，所以我们可以将主对角线上的任意一个数值归一化为1而不影响形状，只有两个值便可表示。这里将右下角的值归一化为一。
最终版本的M矩阵会选择将中间值归一化为一。这样会比右下角归一化出来的5个值更加平缓，数值精度更高。

> - m00和m11模拟材质的粗糙度，其非一致缩放模拟其各向异性。
> - m20和m02为错切变换，模拟偏斜度(skewness)。

---
对于右下角为一的情况。

$$
M =
\begin{bmatrix}
m00 & 0   & m02 \\
  0 & m11 & 0   \\
m20 & 0   & m22
\end{bmatrix}
\overset{normalize}{=\!=\!=\!=\!=}
\begin{bmatrix}
a & 0 & b \\
0 & c & 0 \\
d & 0 & 1
\end{bmatrix}
$$

$$
\det(M) = ac - bcd, \\
M^{-1} = 
\frac{
    \begin{bmatrix}
     c  & 0     & -bc \\
     0  & a-bd  &  0  \\
    -cd & 0     &  ac
    \end{bmatrix}
}{
    ad - bc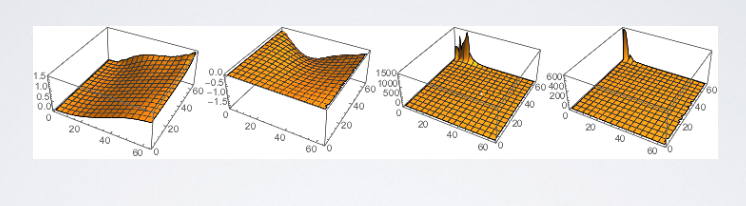
}
$$

![title](/api/file/getImage?fileId=663ee394c6875d1c89a1d8c9)

```
/*
 * a 0 b
 * 0 c 0
 * d 0 1
 * det = ac - bcd
 * adj =  c   0    -bc
 *        0   a-bd  0
 *       -cd  0     ac
 */
float I_ltc_line_width_factor(float3 ortho, float3x3 m_inv)
{
    // transpose(inverse(M)) = (1.0 / determinant(M)) * cofactor(M).
    // Take into account that m12 = m21 = m23 = m32 = 0 and m33 = 1.
    float a = m_inv._11;
    float b = m_inv._31;
    float c = m_inv._22;
    float d = m_inv._13;
    
    float    det = a*c - b*c*d;
    float3x3 cof = {
         c,    0.0,     -b*d,
         0.0,  a - b*d,  0.0,
        -c*d,  0.0,      a*c
    };

// 1.0 / length(mul(V, (1.0 / s * M))) = abs(s) / length(mul(V, M)).
    return abs(det) / length(mul(ortho, cof));
}
```

---
对于中间为一的情况。

$$
M =
\begin{bmatrix}
m00 & 0   & m02 \\
  0 & m11 & 0   \\
m20 & 0   & m22
\end{bmatrix}
\overset{normalize}{=\!=\!=\!=\!=}
\begin{bmatrix}
a & 0 & b \\
0 & 1 & 0 \\
c & 0 & d
\end{bmatrix}
$$

$$
\det(M) = ad - bc, \\
M^{-1} = 
\frac{
    \begin{bmatrix}
     d & 0     & -b \\
     0 & ad-bc &  0 \\
    -c & 0     &  a
    \end{bmatrix}
}{
    ad - bc
}
$$

```
/*
 * a 0 b
 * 0 1 0
 * c 0 d
 * det = ad - bc
 * adj =  d   0    -b
 *        0   ad-bc 0
 *       -c   0     a
 */
float I_ltc_line_width_factor_mid(float3 ortho, float3x3 m_inv)
{
    // transpose(inverse(M)) = (1.0 / determinant(M)) * cofactor(M).
    // Take into account that m12 = m21 = m23 = m32 = 0 and m33 = 1.
    float a = m_inv._11;
    float b = m_inv._31;
    float c = m_inv._13;
    float d = m_inv._33;
    
    float    det = a*d - b*c;
    float3x3 cof = {
         d,   0.0,       -b,
         0.0, a*d - b*c,  0.0,
        -c,   0.0,        a
    };

// 1.0 / length(mul(V, (1.0 / s * M))) = abs(s) / length(mul(V, M)).
    return abs(det) / length(mul(ortho, cof));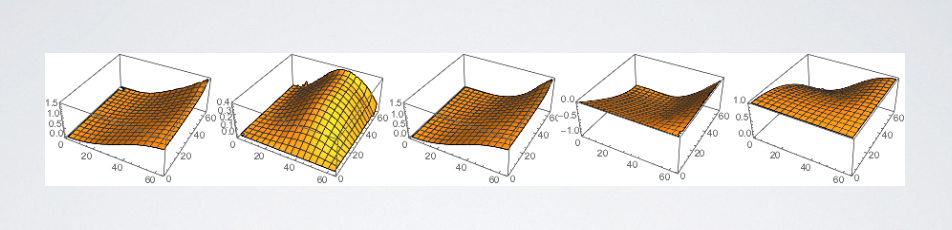
}
```

![title](/api/file/getImage?fileId=663ee36bc6875d1c89a1d8c8)

> - 注意，此处的M为从LUT里读取的最终的矩阵，一般为$M_Inv$，而其逆矩阵(即原始的M矩阵)通常在计算线光源时会用到。

---
## 变换矩阵的用法

我们需要根据不同粗糙度$\alpha$和观察方向$\theta_v$分别计算出一个变换矩阵$M^{-1}$，并将其存储在一张2D纹理中使用，并以$(\alpha, \theta_v)$作为uv采样。
> - 事实上，在真正实现的时候，并不需要真地计算角度之后作为采样uv，而是直接将其cos值作为uv更高效。
![title](/api/file/getImage?fileId=6635c766c6875d1c89a1d830)

我们需要将当前多边形的顶点$P$通过$M^{-1}$逆变换为$P_0$，便可在简单的$D_0$分布下对多边形$P_0$进行积分，等价于在bxdf分布(即$D$分布)下对$P$积分。

## 变换矩阵的求法

该变换矩阵使用下降单纯形法(downhill simplex method, Nelder–Mead method)拟合求得。
该方法使用MIS计算拟合的结果和原始结果的误差，并不断缩小这个误差。

https://blog.csdn.net/myf_666/article/details/129072785

```
// compute the error between the BRDF and the LTC
// using Multiple Importance Sampling
float computeError(const LTC& ltc, const Brdf& brdf, const vec3& V, const float alpha)
{
    double error = 0.0;

for (int j = 0; j < Nsample; ++j)
    for (int i = 0; i < Nsample; ++i)
    {
        const float U1 = (i + 0.5f)/Nsample;
        const float U2 = (j + 0.5f)/Nsample;

// importance sample LTC
        {
            // sample
            const vec3 L = ltc.sample(U1, U2);

float pdf_brdf;
            float eval_brdf = brdf.eval(V, L, alpha, pdf_brdf);
            float eval_ltc = ltc.eval(L);
            float pdf_ltc = eval_ltc/ltc.magnitude;

// error with MIS weight
            double error_ = fabsf(eval_brdf - eval_ltc);
            error_ = error_*error_*error_;
            error += error_/(pdf_ltc + pdf_brdf);
        }

// importance sample BRDF
        {
            // sample
            const vec3 L = brdf.sample(V, alpha, U1, U2);

float pdf_brdf;
            float eval_brdf = brdf.eval(V, L, alpha, pdf_brdf);
            float eval_ltc = ltc.eval(L);
            float pdf_ltc = eval_ltc/ltc.magnitude;

// error with MIS weight
            double error_ = fabsf(eval_brdf - eval_ltc);
            error_ = error_*error_*error_;
            error += error_/(pdf_ltc + pdf_brdf);
        }
    }

return (float)error / (float)(Nsample*Nsample);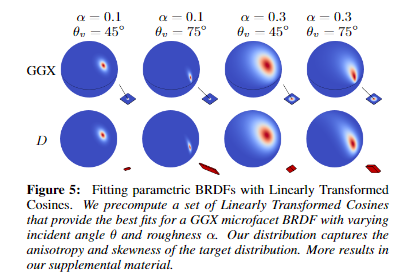
}
```

![title](/api/file/getImage?fileId=6635e746c6875d1c89a1d836)

---
# Integrate

在使用$M^{-1}$将多边形顶点转到cosine分布上之后，便可以在$D_0$上对该多边形进行积分。

但是这里的积分并不是对面积积分，而是对**边**进行积分。

> 这个积分的等价转换有点类似于**斯托克斯定理(Stoke's theorem)**。斯托克斯定理讲的是：在向量场中，场中一个闭合曲线上的线积分等于其所围面积中散度(Curl)的通量(Flux)之和。

$$
    \int_{\Omega} \approx \frac{1}{\pi} \cdot 
    \frac{1}{2} \sum_{i=1}^{n}\arccos(\vec{v_i} \cdot \vec{v_j})
    \frac{\vec{v_i} \times \vec{v_j}}{|| \vec{v_i} \times \vec{v_j} || }
    \cdot \vec{n}
$$

其中i为当前边的起点，j为当前边的终点。如果多边形的边集是以极角排序的，那么将有$j = i \mod n + 1$。

其中$\arccos(\vec{v_i} \cdot \vec{v_j})$为当前边所对应的角度(单位半径下即为弧长)。
![title](/api/file/getImage?fileId=6635bcd5c6875d1c89a1d82b)

其中$\frac{\vec{v_i} \times \vec{v_j}}{|| \vec{v_i} \times \vec{v_j} || }$为当前边与圆心连线组成的扇形面的法线(与该扇形面垂直)。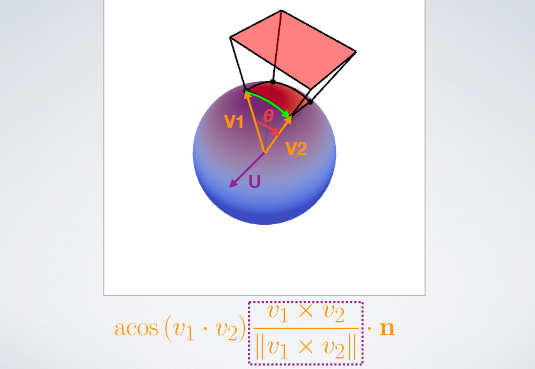
![title](/api/file/getImage?fileId=6635bd1ac6875d1c89a1d82c)

其中$\vec{n}$则为当前着色点的法线，与扇形面的法线的点乘则表示其在当前着色点所在平面的投影，便是最终的radiance。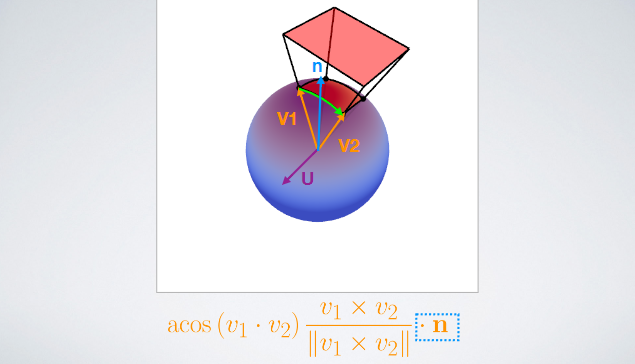
![title](/api/file/getImage?fileId=6635c0f6c6875d1c89a1d82d)

除此之外，在实现的时候，计算$arccos$会有精度丢失从而导致比较明显的瑕疵。论文中的解决方法是通过一个三次函数来近似，当然也有许多其它近似方法。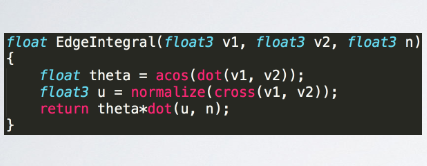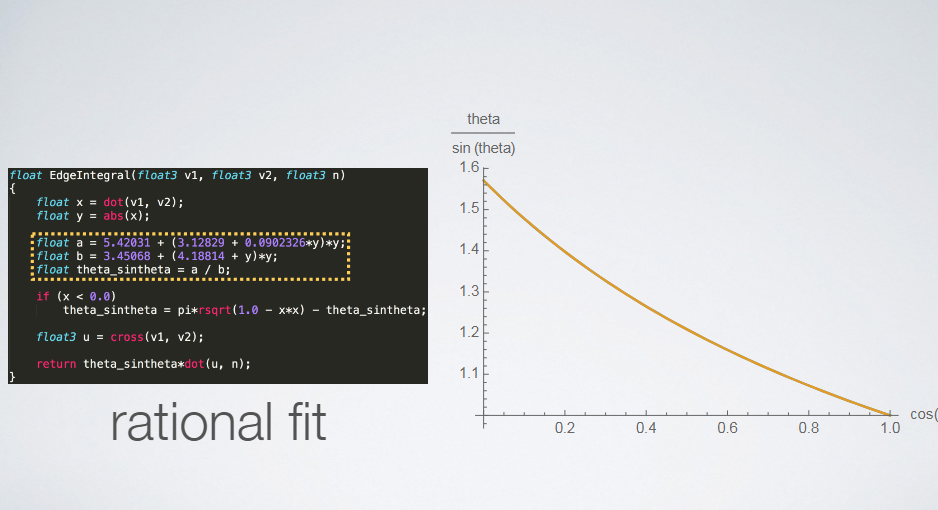
![origin](/api/file/getImage?fileId=6635c6d1c6875d1c89a1d82f)
![approximation](/api/file/getImage?fileId=6635c618c6875d1c89a1d82e)

> - 此处将$\theta$和$\sin(\theta)$一起近似。
> - 这里的$\sin(\theta)$其实是$cross$的长度，即$|| \vec{v_i} \times \vec{v_j} ||$。

---
# clip to horizon(upper hemisphere)

## if-else check

一种方案是每条边与水平面求交，使用交点将水平面以下的边裁掉。这将会产生大量的if-else语句。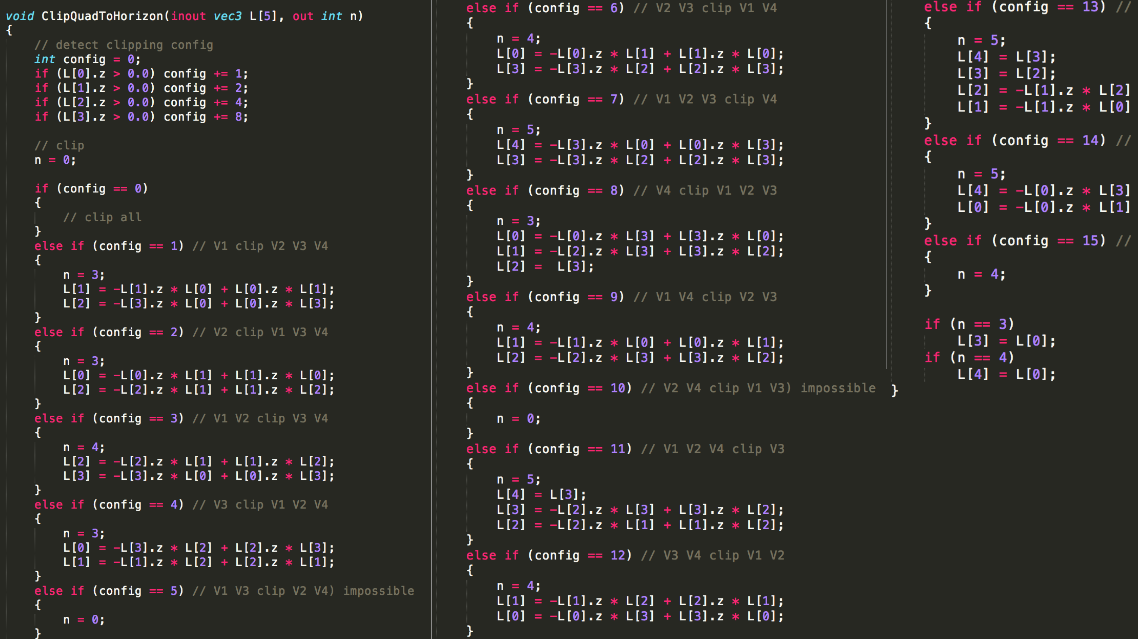
![title](/api/file/getImage?fileId=6635c7f9c6875d1c89a1d831)

## proxy sphere to lut by vector form factor(vector irradiance)。

另一种方案是使用代理体球(proxy sphere)。

该方案重新考察边积分函数，删除与表面法线的点积，从而不投影到平面上，即
$$
    \vec{F} =  \arccos(\vec{v_i} \cdot \vec{v_j})
    \frac{\vec{v_i} \times \vec{v_j}}{|| \vec{v_i} \times \vec{v_j} || }
$$

由此可得一个向量，称为向量辐射度(vector irradiance)$\vec{F}$。

$\vec{F}$的模长但是光源在$\vec{F}$方向上的irradiance大小。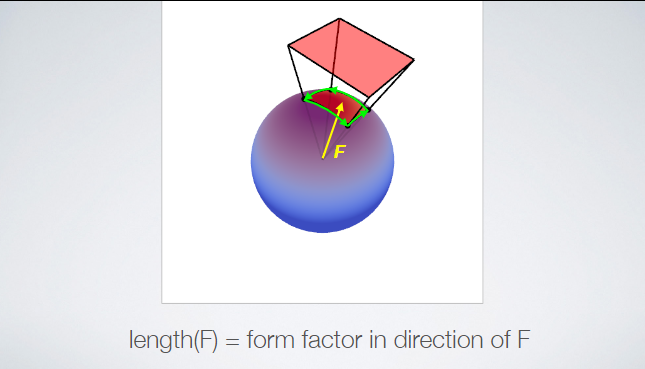
![title](/api/file/getImage?fileId=6635d874c6875d1c89a1d832)

由于我们可以假设irradiance大小为$||\vec{F}||$的光源来自一个球体。且可以通过$\vec{F}$获得一个该球体对于当前cosine分布的张角(angular extent)和倾斜度(elevation angle)。
$$
\left\{
\begin{array} \
    angular\_extent = \arcsin\sqrt{|| \vec{F} || } \\
    elvation\_angle = \vec{n} \cdot \frac{\vec{F}}{|| \vec{F} ||}
\end{array}
\right.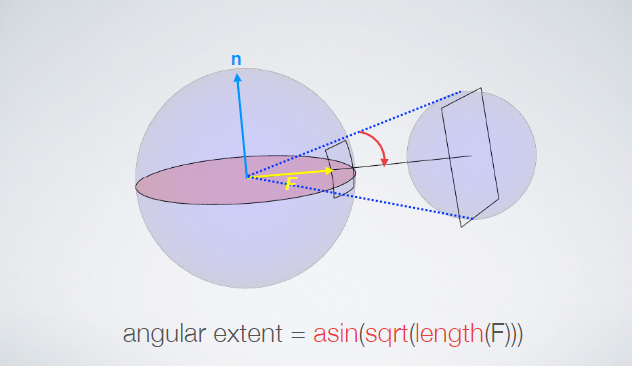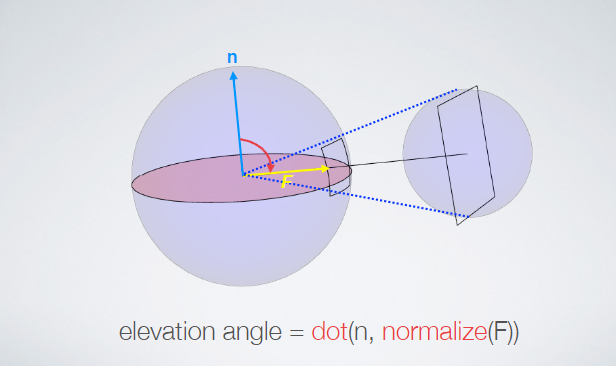
$$

![title](/api/file/getImage?fileId=6635de24c6875d1c89a1d833)

![title](/api/file/getImage?fileId=6635de29c6875d1c89a1d834)

对于不同的张角$(\sigma \in (0, \frac{\pi}{2}))$，和不同的倾斜度$(\omega)$。我们可以离线求出裁剪后的radiance结果大小，从而获得裁剪后与未裁剪的比例，并将其存储到一张2D Lut贴图上，并在运行时根据张角和倾斜度计算uv进行采样即可。

其中计算裁剪后的radiance结果可参考下图。

![title](/api/file/getImage?fileId=6635e1c7c6875d1c89a1d835)

该方法根据倾斜度和张角确定的范围与半球的关系分为4类。

> - 最下方边缘处的倾斜角也小于90度，说明没有在水平面以下的情况。
>   - 即$\omega + \sigma < \frac{\pi}{2}$。即$\omega \in [0, \frac{\pi}{2} - \sigma]$。

> - 最下方边缘处的倾斜角大于90度，但中间的倾斜角(即$\omega$)小于90度。
>   - 此时有一半以上在水平面以上，但有一部分在水平面以下。
>   - 即$\omega + \sigma > \frac{\pi}{2}$且$\omega < \frac{\pi}{2}$。
>   - 即$\omega \in [\frac{\pi}{2} - \sigma, \frac{\pi}{2}]$。

> - 中间倾斜角大于90度，但最上方边缘处的倾斜角小于90度。
>   - 此时有小于一半在水平面以上，有一半以上在水平面以下。
>   - 即$\omega > \frac{\pi}{2}$且$\omega - \sigma < \frac{\pi}{2}$。
>   - 即$\omega \in [\frac{\pi}{2},\frac{\pi}{2} + \sigma]$。

> - 最上方边缘处的倾斜角也大于90度，中间倾斜角小于180度。
>   - 此时所有都在水平面以下。
>   - 即$\omega - \sigma > \frac{\pi}{2}$。
>   - 即$\omega \in [\frac{\pi}{2} + \sigma, \pi]$。

```
float ihemi(float w, float s)
{
    float g = asinf(cosf(s)/sinf(w));
    float sinsSq = sqr(sinf(s));

if (w >= 0.0f && w <= (pi/2.0f - s))
        return pi*cosf(w)*sinsSq;

if (w >= (pi/2.0f - s) && w < pi/2.0f)
        return pi*cosf(w)*sinsSq + G(w, s, g) - H(w, s, g);

if (w >= pi/2.0f && w < (pi/2.0f + s))
        return G(w, s, g) + H(w, s, g);

return 0.0f;
}
```

---
# fresnel approximation

由于没有考虑能量的遮蔽和吸收，上面的LTC积分的结果始终为1。

也就是说，LTC积分只考虑了bxdf的形状，但是并没有考虑其大小，我们需要考虑Fresnel项求其大小。

这个过程跟IBL里求DFG那张LUT有些类似。最终的$n_D$和$f_D$项也序列化到一张2D Lut上，根据roughness和NoV采样即可。

![title](/api/file/getImage?fileId=6635e859c6875d1c89a1d837)

> - 这里也可以存储$n_D-f_D$和$f_D$，从而减少一次乘法。
> - 这张LUT和水平裁剪的那张LUT可以合并在一起。

---
# shading with textured polygonal lights

todo...

---
# ref

> - Real-Time Area Lighting
https://blog.selfshadow.com/publications/s2016-advances/s2016_ltc_rnd.pdf

> - https://zhuanlan.zhihu.com/p/345364404
> - https://zhuanlan.zhihu.com/p/426217725
> - https://zhuanlan.zhihu.com/p/350694154

> - Projective Texture Mapping
https://developer.download.nvidia.cn/assets/gamedev/docs/projective_texture_mapping.pdf

> - learn opengl area light
https://learnopengl-cn.github.io/08%20Guest%20Articles/2022/03%20Area%20Lights/#_9

> - self shadow ltc github code
https://github.com/selfshadow/ltc_code

> - LTC Fresnel Approximation
https://blog.selfshadow.com/publications/s2016-advances/s2016_ltc_fresnel.pdf

> - sphere / disk light by ltc
https://blog.selfshadow.com/publications/s2017-shading-course/heitz/s2017_pbs_ltc_lines_disks.pdf
[sig17][arealight][disk light]Real-Time Line- and Disk-Light Shading with Linearly Transformed Cosines.pdf

Navigation

Recent Posts

Friend Links